树
树(tree)是一类比较重要的非线性的数据结构。之所以叫“树”,是因为它看起来像是一棵倒挂的树,根朝上,叶朝下。
树的基本哲学
树,是一种递归定义的数据结构。
树的相关概念
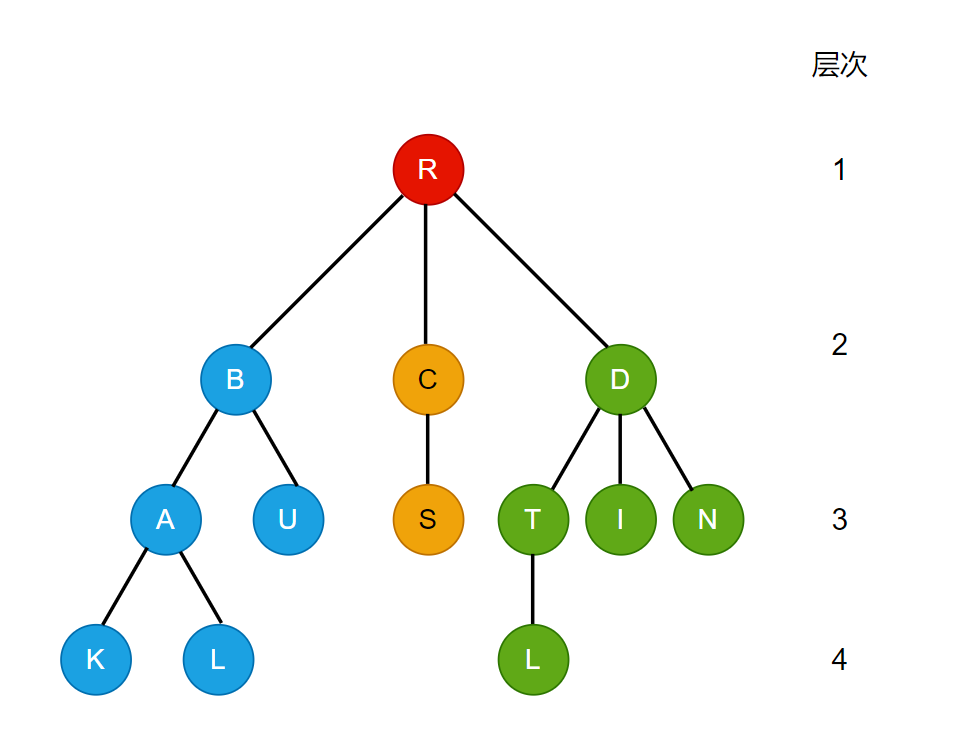
以上图为准,下面介绍相关概念:
- 节点:树中每一个字母代表的区域都可以称为节点。
- 根节点:一棵树只有一个
根节点(root),例如图中的R。 - 子树:假设有蓝色部分的树1={B, A, U, K, L}, 黄色部分的树2={C, S}, 绿色部分的树3={D, T, I, N, L}。那么,树1,2,3,都称为是以R为根的树的子树。其中树1又有以A为根节点的{K, L}和以B为根节点的{U}等若干个子树,所以树是递归定义的。一棵树包含若干子树,子树里面可能又有子树,子子孙孙~
- 节点的度:一个节点含有的子树的个数。比如节点R与D的度为3,B和A的度为2,C和T的度为1, K、L、U等节点的度为0。
- 叶结点:也叫终端节点,是指度为0的节点。比如, S、L、I、N、还有前面提到的K、L、U。
- 非终端节点:也叫分支节点,是指度不为0的节点。
- 父节点与子节点:父节点也叫双亲节点,子节点也可以叫做孩子。一个节点的子树的根称为该节点的孩子,以根节点为例,R的子树有树1,2,3,这三棵子树的的根节点分别为B,C,D,都是根节点R的子节点,同时该节点称为孩子的父节点,也即R是B,C,D的父节点。其他子树也同理。
- 兄弟节点:具有相同父节点的节点互称为兄弟节点;比如,A和U互称兄弟节点,T,I,N等。
- 祖先和子孙: 祖先是指,从根节点到该节点所经分支上的所有节点。比如L的祖先为T,D,R。子孙是指,以某节点为根的子树中任一节点都称为该节点的子孙。比如,B的子孙有A,U,K,L。
- 节点的层次:根为第1层,根的孩子为第2层,以此类推。
二叉树
二叉树(Binary tree)是指树中节点的度不大于2的有序树,当节点数为0时,是一棵空树,否则为非空树。它是数据结构中的重点研究对象。
有如下特征或性质:
- 根节点只有一个
- 每个节点至多有两棵子树,如果有两棵子树,左边的叫左子树,右边的叫右子树。
- 子树有左右之分,次序不能随意颠倒。
- 二叉树也是递归定义的,如果一个节点有子树,那么这个子树本身又是一棵二叉树。
二叉树的遍历
下图是一个以节点A为根的二叉树:

再提树的基本哲学
还记得前面我说的树是一种递归定义的数据结构吗?带着这种思想来学习二叉树树的遍历吧。
前序遍历
前序遍历(Pre-Order Traversal)的次序为:根 -> 左 -> 右。
- 从根节点出发,访问根节点,得到 A。
- A有左右子树,按照次序,应该访问左子树,得到 U。
- 以U为根,它又有左右子树,按照先序遍历顺序,这时候应该再次访问U的左子树,得到T。
- T没有子节点,因为是递归,而刚才以U为根节点,遍历了它的左子树,所以回到U。
- 现在开始遍历U的右子树,得到 I。
- 然后回到A,以A为根,刚才遍历了A的左子树,现在开始同样以
根 -> 左 -> 右的次序遍历A的右子树即可。
最后可以得到前序遍历的结果:A -> U -> T -> I -> S -> N -> X, 也即是从A出发,沿着这棵树的外围绕了一圈,但重要的思想还是:树是递归定义的数据结构。
当先序遍历一棵二叉树时,根节点总是在第一个。
中序遍历
中序遍历(In-Order Traversal)的次序为:左 -> 根 -> 右。
- 从根节点出发,有左右子树,前进到左子树U。
- U还有左右子树,继续前进到T,T没有子节点,得到 T。
- 根据递归与中序遍历次序,轮到“根”了,得到 U。
- 然后是“右”,得到 I。
- 这样A的左子树就遍历完了,到“根”了,得到 A。
- “左”和“根”都已经遍历完毕,再按照中序遍历的次序遍历“右”即可。
最后可以得到中序遍历的结果:T -> U -> I -> A -> N -> S -> X。当中序遍历一棵满而二叉树(比如上图中的树)时,根节点总是在结果的中间。
后序遍历
后序遍历(Post-Order Traversal)的次序为:左 -> 右 -> 根。
- 从根节点A出发,沿着左子树往下走直到一个终端节点,得到T。
- 按照后序遍历次序,得到I。
- 然后U.....
最后可以得到后序遍历的结果:T -> I -> U -> N -> X -> S -> A。后序遍历一棵二叉树,根节点总是在最后一个。
层次遍历
层次遍历很简单,按照层次,从上到下,从左到右。
层次遍历的结果是:A -> U -> S -> T -> I -> N -> X.
二叉树的节点
/* 树的节点 */
typedef struct tree_node {
/* 左孩子指针 */
struct tree_node *left;
/* 右孩子指针 */
struct tree_node *right;
/* 关键字 */
char key;
}tree_node;这个结构体定义了指向树的节点的左右指针,以及一个char类型的关键字, key。
二叉树节点的创建
/* 创建一个节点 */
tree_node *tree_create_node(char key)
{
tree_node *node = (struct tree_node*)malloc(sizeof(struct tree_node));
if(node==NULL) return NULL;
node->key = key;
node->left = NULL;
node->right = NULL;
return node;
}上面的方法,接收一个关键字(key)作为参数,然后使用创建一个二叉树的节点并初始化,最后返回指向该节点的指针。
二叉树的创建
/* 创建一棵二叉树 */
tree_node *tree_create()
{
char str;
tree_node *current;
scanf("%c", &str);
if('#' == str)
{
current = NULL;
}
else {
current = tree_create_node(str);
current->left = tree_create();
current->right = tree_create();
}
return current;
}递归法创建一颗二叉树。
- 定义一个char类型变量str,和一个节点指针current。
- 等待用户输入,并将输入的字符赋值给 str。
- 用
#表示空节点,按照先序遍历的次序,生成二叉树。
注意,使用该函数时,用户一次输入一颗完整的二叉树。 比如:
ABD##E##CF##G##按道理,递归创建,该函数会被自己多次调用,我们就应该输入多次,以表示节点的字符。但由于我们在最开始一次输入完了,所以每次scanf函数都会从缓冲区读取一个字符并执行程序。
最后我们成功创建了一颗如下的二叉树:


递归法遍历二叉树
这里函数不仅可以遍历一颗完整的二叉树,还可以遍历以参数节点为根节点的子树。
看这段程序,只需要记住树的基本哲学是递归,以及对应的遍历次序即可。
/* 前序遍历 */
void preorder_traverse1(tree_node *node)
{
if(node != NULL) {
printf("%c\t", node->key);
preorder_traverse1(node->left);
preorder_traverse1(node->right);
}
}
/* 中序遍历 */
void inorder_traverse1(tree_node *node)
{
if(node != NULL) {
inorder_traverse1(node->left);
printf("%c\t", node->key);
inorder_traverse1(node->right);
}
}
/* 后序遍历 */
void postorder_traverse1(tree_node *node)
{
if(node != NULL) {
postorder_traverse1(node->left);
postorder_traverse1(node->right);
printf("%c\t", node->key);
}
}非递归法遍历二叉树
非递归法主要是利用了栈来实现(模拟递归,其实函数的递归本身就是栈实现的),这里我们直接用前面章节实现的栈就可以。
代码中别忘了把之前写好的
stack.h与stack.c放入当前目录中,并且写好头文件包含:
#include "stack.h"非递归法前序遍历二叉树的思路:
- 定义一个称为指向当前节点的指针current。
- 从根节点出发,即current=root,沿着current的左子树(如果有)往下走,并把current的根节点压入到栈中。
- 循环上述过程,直到叶子节点。
- 出栈,并将current置为出栈的节点的右子树,再回到步骤1,循环执行。
- 循环的终止条件是:当前节点为空或栈为空。
沿着这个思路就很容易实现非递归前序遍历:
/* 前序遍历2 */
void preorder_traverse2(tree_node *node)
{
stack *stack = stack_create();
tree_node *current = node;
while (current != NULL || stack->length)
{
if(current != NULL) {
printf("%c\t", current->key);
stack_push(stack, current);
current = current->left;
} else {
current = stack_pop(stack);
current = current->right;
}
}
stack_release(stack);
}非递归中序遍历也是用栈来实现,思路大致相同:
/* 中序遍历2 */
void inorder_traverse2(tree_node *node)
{
stack *stack = stack_create();
tree_node *current = node;
while (current != NULL || stack->length)
{
if(current != NULL) {
stack_push(stack, current);
current = current->left;
} else {
current = stack_pop(stack);
printf("%c\t", current->key);
current = current->right;
}
}
stack_release(stack);
}非递归后序遍历略有不同,这里用的是较为简单的思路:双栈。
第一个栈用根 -> 右 -> 左的顺序非递归遍历二叉树,利用第二个栈把结果反过来,就是后序遍历的顺序左 -> 右 -> 根,妙不?
/* 后序遍历2 */
void postorder_traverse2(tree_node *node)
{
stack *s = stack_create();
stack *stack = stack_create();
tree_node *current = node;
while (current != NULL || stack->length)
{
if(current != NULL) {
stack_push(s, &(current->key));
stack_push(stack, current);
current = current->right;
} else {
current = stack_pop(stack);
current = current->left;
}
}
while (s->length)
{
printf("%c\t", *(char *)stack_pop(s));
}
stack_release(s);
stack_release(stack);
}层次遍历二叉树
层次遍历一颗二叉树,比较简单,利用队列。这里也用前面章节写好的就行。
代码中别忘了把之前写好的
queue.h与queue.c放入当前目录中,并且写好头文件包含:
#include "queue.h"层次遍历的基本思路:
- 从根节点出发,把根节点放到队列中
- 队列出队,输出出队节点的关键字。
- 判断出队节点是否有左右孩子,如果有就按照,从左到右的顺序将节点加入队列。
- 回到步骤2,往下执行,直到队列为空,遍历终止。
/* 层次遍历 */
void level_traversel(tree_node *root)
{
/* 创建一个队列 */
queue *queue = queue_create();
if(root != NULL)
{
queue_push_data(queue, root);
}
while (queue->length)
{
tree_node *current = queue_pull_data(queue);
printf("%c\t", current->key);
if(current->left) queue_push_data(queue, current->left);
if(current->right) queue_push_data(queue, current->right);
}
/* 队列用完后,释放 */
queue_release(queue);
}编译并测试
测试函数写在main函数中。
int main() {
/* ABD##E##CF##G## */
tree_node *root = tree_create();
printf("\n前序遍历1:");
preorder_traverse1(root);
printf("\n前序遍历2:");
preorder_traverse2(root);
printf("\n\n中序遍历1:");
inorder_traverse1(root);
printf("\n中序遍历2:");
inorder_traverse2(root);
printf("\n\n后序遍历1:");
postorder_traverse1(root);
printf("\n后序遍历2:");
postorder_traverse2(root);
printf("\n\n层次遍历0:");
level_traversel(root);
printf("\n");
return 0;
}编译命令:
# gcc *.c && ./a.out输入:
ABD##E##CF##G##输出:
前序遍历1:A B D E C F G
前序遍历2:A B D E C F G
中序遍历1:D B E A F C G
中序遍历2:D B E A F C G
后序遍历1:D E B F G C A
后序遍历2:D E B F G C A
层次遍历0:A B C D E F G
中序遍历 似乎不对 T -> I -> U -> A -> N -> S -> X
抱歉,确实错了。感谢你指出错误,已修改。